|
Мога да правя добре няколко неща, но най-добър съм в забравянето. Като ученик не можех да науча едно стихотворение наизуст, защото докато науча края му, забравях началото. Да, но научих нещо, което другите не успяха:
Красотата не е в рецитирането на поезия, а в четенето на поезия и особено - в писането на поезия. Да рецитират могат и папагалите.
0 Comments
Според теорията размерът няма значение, а между цевта на пушката и геврека няма разлика. На жаргона на тополозите - цевта и геврекът са хомеоморфни.
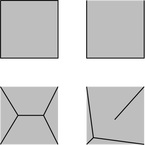
Според Айнщайн, на теория няма разлика между практика и теория, но на практика - има. Та затова ... ако питате мен, ще ви кажа че, независимо от това какво казва теорията, в практиката ситуацията е следната: Ще ти кажат че размерът няма значение пушките с късите цеви, но не и гевреците с големите дупки. Има един проблем, който от 101 години се опъва на световната математика. Нарича се "Проблемът с непрозрачната гора" (Opaque forest problem). Ще се опитам да го опиша с мастило за първи клас: Наследил съм квадратно парче земя със страна 1. За да го предпазя от лошите очи на съседите, аз трябва да го оградя. Целта е: 1. съседски поглед да не може да премине през земята ми и 2. оградата да е с минимална дължина (за по-евтино). Формата и броя на сегментите на оградата, както и това дали сегментите са свързани един с друг или не, е по мой избор (стига да може да се изчисли дължината на оградата). Ако искаме да опишем проблема с мастило за втори клас, то можем да сменим "квадрат" с "изпъкнал многоъгълник". Но за момента това не е толкова толкова важно, затова илюстрациите ще са с квадрати.  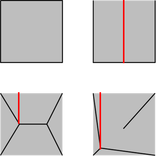Източник: Уикипедия, Автор: Alexis Beingessner Давам няколко примерни решения с дължина на оградата d: а) горе вляво: d=4, б) горе вдясно: d=3, в) долу вляво: d≈2.73, г) долу вдясно: d≈2.64. Решението г) за момента се приема за оптимално, въпреки че това още не е доказано. Лесно можем да забележим че в някои от решенията, ако се объркаме и останем в имота, то без да разваляме/прескачаме оградата нямаме път за навън (или пък пътят е неприятно дълъг). Затова нека да модифицираме проблема така: Спазвайки изискванията да не разваляме оградата и да не я прескачаме, коя е минималната сума от дължините на: 1) оградата (черни линии) и 2) пътя от точката, максимално отдалечена от незаградена страна на имота, до същата страна (червени линии)? Тук нещата са по-различни: сумарната дължина на черни и червени линии при вариант в) е по-къса от тази при вариант г). Съществува ли вариант с още по-малка сумарна дължима?  Източник: Уикипедия, Автор: Alexis Beingessner, Модификация: моя милост Журналистка попитала Далай Лама кога е бил най-щастлив, а той с чистосърдечна усмивка отговорил: "Сега, точно в този момент". Странно, ще речеш че мечтата му от малък е била да дава интервюта. Това ми прилича на мечта на поп-звезда или политик. Всъщност, не е ли Далай Лама точно такъв?
Защо казваме че църквата ни е православна, след като тя през повечето време не е права и почти никога не е славна?
Понеже днес съм настроен на вълна афористи и афоризми, та не може да не ми направи впечатление сходството в начина на мислене на афористите-политици.
Владимир Илич Ленин Дайте ни дете за 8 години и ние ще ви дадем комунист завинаги. Адолф Хитлер Който владее младежта, той печели бъдещето. Румен Радев (в Париж) Трябва да спечелим умовете и сърцата на младото поколение. Не виждаш сходството, ли? Елементарно, Уотсън, политиците-печалбари обичат да печелят от сделки с младежта. Човек, който не прави разлика между афорист и аферист, не владее езика си. Човек, който прави разлика между афорист и аферист, но не вижда че често аферистите са и афористи, не владее зрението си.
Афористи са били: Адолф Хитлер Голямата сила на тоталитарната държава е в това че тя кара тези, които се страхуват от нея, да я имитират. Владимир Илич Ленин Свободата е толкова ценна, че трябва да бъде разпределяна много пестеливо. Йосиф Сталин В Съветската армия се иска повече смелост да отстъпиш, отколкото да нападнеш. С македонците си приличаме по езика и по претенциите. Те претендират че са владели света политически - заради Александър Македонски, с когото нямат нищо общо. Ние претендираме че сме го завладели културно - заради Кирил и Методий, с които също нямаме нищо общо.
Онзи ден, покрай "френския" полет на президента ни, се бях замислил що за щура страна сме. Плащаме луди пари за охраната му, за да е добре въоръжена с: автоматични оръжия, бронирани мерцедеси, модерни комуникации и какво ли още не. И за какво? За да го опазят от риска да не го наплюе или шамароса някой разгневен съгражданин? А в същото време президентът се излага на риск, връткайки кръгчета на френски изтребител, на какъвто никога преди не е летял. Не че наскоро е летял на нещо. Не че би трябвало, нали е президент за да президентства, не за да лети. Чувствам че не сте съгласни с мен, та затова ще добавя че нито Барак Обама водеше лекции на юристи през уикендите, нито Доналд Тръмп сключва сделки с апетитни недвижими имоти по време на президентските си визити в чужбина.
Днес чета последната творба на Дан Браун, където се описва испанската Кралска гвардия, грижеща се за сигурността на краля и семейството му. Решавам да проверя що за животно е тя и Уикипедия уставно докладва: подразделение на въоръжените сили с напълно военни функции и подготовка, наброяващо 1900 души и включващо десантчици и артилерия. Или Испания е по-щура страна от нашата, или и там има много мераклии да им плюят и шамаросват величествата. Сещам се че има една област, която плюе не само на величеството, ами на цялата испанска монархия. Охрани, всуе се морите! Let k be a non-negative integer, n be a positive integer and  be the sum of the k-th powers of the positive integer divisors of n. Let  be the sum of the k-th powers of the odd positive integer divisors of n. Is it true that for every nonnegative integer k and positive integer n the latter sigma divides the former sigma ? In other words, is it true that for every k and n  Понеже днес е студентският празник, а и пак се сетих за мисълта на Насим Талеб че университетите се отнасят към образованието така, както проституцията се отнася към любовта, та .....
Преди време имаше момче-журналистче на име Майкъл Гладуел, което беше станало популярно по целия свят с писанията си. В България едни олигарси даже бяха нарекли групичката си на негова книга. Момчето още го има, но популярността му намаля. Започнаха да го подиграват, излезе му име на "най-добре платеният разказвач на приказки". В една от книжките си ("Изключителните: История на успеха"), туй момче беше посветило място на лековат анализ на най-интелигентния американски мъж - Кристъфър Ланган. Ланган не завършил следването си и работил като строителен работник, каубой и горски стражар, а после (в продължение на две десетилетия) - като бияч в заведения. "Провалът" му в университета и живота, според журналистчето, се дължал на слабата му емоционална интелигентност, а тя - на лошия му произход. Тази работа с емоционалната интелигентност е дело на друго момче-журналистче на име Даниел Голман. И при него ситуацията е подобна: изкара луди пари от популяризирането на чужди теории, въпреки че ентусиазмът му не се споделяше дори от авторите на теориите. Днес, 22 години след неговата "Емоционална интелигентност", ненаучността и неефективността на концепцията "емоционална интелигентност" не е тайна за никого (линк). Но да се върнем към университетите и да видим как те понякога са лошо място не само за суперинтелигентните студенти като Ланган, но и за суперинтелигентните учени. Робърт Тривърс бе професор в американски топ-университети, като се започне с Харвард и се свърши с Ратгърс. Автор е на концепциите за "реципрочния алтруизъм" и "себичния ген". След 47-годишна научна кариера, оставила отпечатък върху хиляди студенти и учени, сред които Стивън Пинкър, О. Е. Уилсън и Ричард Докинс, Тривърс е освободен от Ратгърс защото се противял да води лекции в дисциплина, в която не е специалист. Опитите на Тривърс да откаже лекциите не само били безуспешни, били безуспешни дори опитите му да се срещне с ръководството на университета за да представи аргументите си. Какво ли биха казали на Тривърс журналистчетата Гладуел и Голман: Как можа да си толкова неинтелигентен бе, Тривърс? Ръководствата на университетите са за да набират пари от инвеститори и дарители, и след това да решават как да ги харчат, а не за да се срещат с разни професори! Това е то! В днешните неинтелигентни времена, интелигентността се мери не с Коефициент на интелигентност или със Списък на откритията, ами с това колко пари можеш да изкараш и похарчиш. Децата у нас четели по-добре от връстниците си в САЩ и Германия. Прекрасно, само дето четенето е като правенето на зехтин. Химическата технология извлича по-добре зехтина от маслините в сравнение със студеното пресоване, но ... ох, какъв парадокс ... химически полученият зехтин е по-лош от студено-пресования. Заради което е по-евтин.
Ако мисълта ми изглежда усукана, ще я изправя: не е важно само колко добре четеш, но и какво имаш на разположение за четене. Вземете за сравнение български и американски учебници по счетоводство. От американския можеш да научиш почти всичко за счетоводството, от българския - само две неща: а) колко не разбира от счетоводство авторът, и б) колко неспособен е да предаде на студента дори това, което разбира. Защо поговорките винаги вървят по двойки? Едната казва едно, а другата - точно обратното? Например:
а) Кови желязото докато е горещо срещу Бързата кучка слепи ги ражда, б) Който се учи, той ще сполучи срещу Не можеш да научиш свинята да пее, но можеш да скъсаш нервите и на двамата докато се опитваш. За мен нещата са очевидни: едни поговорки са дело на оптимисти, а други - на песимисти. Кой от подходите върши повече работа в "случая с ученето"? Всеки би могъл да проведе следния експеримент в главата си или вън от нея: Сформирай чрез случаен подбор 2 групи: на неучилите и на свините, учени да пеят! Установи относителния дял на неучилите, които са сполучили и на свините, които пеят! Елементарно, Уотсън: има много неучили които са сполучили, но няма нито една свиня научена да пее (колкото и да са се мъчили учителите). Е, схвана ли идеята? Установи ли преимуществото на песимизма по отношение на вярата в образованието? Ако не си, то дали не прекаляваш с оптимизма? Или пък имаш дупки в образованието? Затова ще завърша със следния парадокс: Съмнения в образованието (и образованието си) имат предимно хората с добро образование. Петима другари седнали на кръгла маса да бистрят международното положение. Всеки направил по 3 поръчки: питие, мезе и десерт. Ачо и Кочев поръчали вино, Бочо и Бочев – бира, а Ачев – ракия. Ачо и Дочев поръчали босненска салата, а Кочо и Ачев – албанска салата. Кочо и Енчев си поръчали торти, а Дочо и Ачев – баклава. Един си поръчал щрудел.
Когато келнерът донесъл поръчките, направило му впечатление че никоя двойка съседи по маса няма еднаквa поръчка, била тя напитка, мезе или десерт. Кой си е поръчал шопска салата и какви са другите му поръчки? |
Categories
All
Archives
November 2023
|
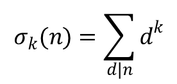
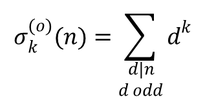
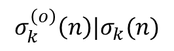
RSS Feed
