Blog Archives

Бизнес модели

8/20/2012

Безизходицата е съдба на хората без въображение. Житейските проблеми са решими, понякога по няколко различни начина. Днес ще го демонстрираме, сравнявайки бизнес модела на "Жилет" с този на "Уилкинсън".*

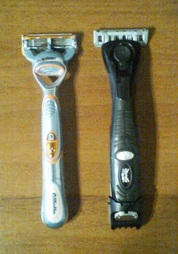
"Жилет" залагат на "нарко-модела", масово използван от лидерите, без значение дали те произвеждат автомобили или копирни машини: зарибяваш жертвата с ниски цени и след това я доиш до болка с консумативите. Самобръсначката е сравнително евтина, но се налага честа смяна на ножчетата, които са скъпи. Моята "балканска подсилена" брада убива ножчето на "Жилет" за 2 седмици.

Бизнес моделът на "Уилкинсън" е с човешко лице: продават ти по-евтина самобръсначка с много по-евтини ножчета. Къде е "врътката"? Ножчетата траят не по 2 седмици, а по 3 месеца. Продадеш ли на един мъж самобръсначка "Уилкинсън", той (ако не е рекламно лице на "Жилет" или малоумен) никога няма да премине към конкурента (освен ако конкурентът не подобри и поевтини продукцията си драстично). Казано накратко, за да победиш в конкурентната война няма нужда да продаваш милиони ножчета на един мъж; трябва само да продадеш милиони самобръсначки - по една на всеки мъж. Елементарно, Уотсън, разумният мъж има нужда не от милиони ножчета, а просто от една самобръсначка.

___________________________________________________________________
* в лицето на "моторизираните" им варианти Gillette Fusion Power и Wilkinson Sword Quattro Titanium

0 Comments

What does ABSTRACT ART mean?

8/19/2012

0 Comments

Is abstract art an abstract representation of real objects/processes or a "realistic" representation of abstract objects/processes? Almost no one will consider the latter type of art abstract. Botticelli painted The Birth of Venus realistically and everybody looking at it forgets that Venus is something abstract.

The blue thing below is a painting of mine which I named "The Birth of Square Numbers from the Triangular Numbers". If you have problems seeing the square numbers (1, 4, 9 and 16), then count the white triangles (each one of which is marked by a red dot) between any three blue circles. If you have problems seeing the triangular numbers (3, 6, 10 and 15), you are probably blind.

The painting makes easy to see some abstract things.
4=1+1+2 and 9=1+1+2+2+3.
In fact, for any natural number n the corresponding square number
n^2=1+1+2+2+...+(n-1)+(n-1)+n
Therefore, you can easily see that the n-th square number is the sum of the n-th and (n-1)-th triangular numbers. Does this make my painting abstract or not?

0 Comments

How I proved the Pythagorean theorem, 1

8/16/2012

0 Comments

Everybody can prove the Pythagorean theorem, but have you seen a proof as short as mine is?

Всеки може да докаже Питагоровата теорема, но виждали ли сте доказателство, кратко като моето?

0 Comments

Goldbach calculator, 1

8/15/2012

0 Comments

Insight can emerge from failure to acccomplish something else. Gerd Gigerenzer

Following my naive attempt to prove Goldbach’s conjecture, I found an algorithm for calculating the Goldbach’s partitions. The calculator you can see HERE is created (based on the same algorithm) by the talented programmer, engineer, photographer and aviation historian Plamen Antonov.

They say a picture is worth a thousand words. See on the left Plamen's picture of my words.

Here's my algorithm for the Goldbach calculator:
Step 1. Take Х (an even number greater than 4) and divide it by 2.
Step 2. If the halves X/2 are even go to Step 3, otherwise go to Step 4.
Step 3. Add 1 to the first half, and subtract 1 from the second half.
Step 4. If X1 and X2 (the numbers resulting from Steps 2, 3 and 5) are prime, print X1 and X2.
Step 5. If X2=3 stop, otherwise add 2 to X1, subtract 2 from X2 and go to Step 4.

P.S. 1
In the language of Wolfram Mathematica my approach

gold[x_]:=Module[{lst={},h=x/2},While[h>1,If[PrimeQ[h]&&PrimeQ[x-h],AppendTo[lst,{h,x-h}]];h--];lst];
gold[1787834]//AbsoluteTiming

works much faster than those based on IntegerPartitions or FrobeniusSolve functions (see the musings of some experts here).

P.S. 2
f[n_]:=PrimePi[n/2];
g[n_]:=Module[{lst={}}, Do[If[PrimeQ[n-Prime[i]],AppendTo[lst,{Prime[i],n-Prime[i]}]],{i,1,f[n]}];lst];
g[1787834]//AbsoluteTiming

works much faster than its "older sibling" mentioned in P.S. 1.

P.S. 3
June 22, 2020
Who could have known that one day this would be called Ianakiev's Algorithm?

0 Comments

Оградата на Патриарха

8/12/2012

0 Comments

Монолог а'ла Габриел Гарсия Маркес и Стефан д-р Чолаков

Настана време неЧЛЕНоразделно и социалистите са зарязали почитането на паметта на най-личния им ЧЛЕН - бай Гошо Консервата, комуто навремето (и приживе, и посмъртно) всеки техен ЧЛЕН беше длъжен да прави теманета a la turque и челoбитни a la russe, че и това не им беше достатъчно, ами караха и нас да се навеждаме, но и те като нас изневериха на култа към ЧЛЕНа на личността и вече не бръснат бай Гошо за СЛИВА, та са зарязали всякаква поддръжка на историческия му дом, и особено на историческата му ограда, вместо да вземат да съберат по някой лев от ЧЛЕНовете си, на които няма да им се счупят ЧЛЕНовете ако вземат та поправят счупената ограда на дома на бай Гошо на ул. "ОпиЧЛЕНска" за да не ни е срам от капиталистическите СЛИВИ, които може "случайно" да се окажат с гадните си капиталистически камери в тези мръсни ЗАДНИ ЧАСТИ на София за да заснемат срама ни и да го изтъпанят по БиБиСи за срам на всички ЧЛЕНове на прогресивното човечество, които най-накрая ще разберат, че у нас е настанало време неЧЛЕНоразделно, та от ламтеж за катерене по стълбите социалистите са забравили изобщо за мазетата, покривите и (както се вижда) оградите, полегнали като ЧЛЕНовете на ЧЛЕНската им маса, чиято деменция ѝ пречи да си дигне ЗАДНИКА и да си го разходи до дома на този, за когото всички знаехме, че МУ е прав и СЛЕД като съгреши дори, ама на кого му пука дали му е прав или не след като оградата му е полегнала на една страна и ще падне така, както ще падне и родния му дом, така както падна и "вечния" му дом, въпреки че на ония меки сини СЛИВИ им трябваше една седмица за да го бутнат.

0 Comments

Бизнес модели

What does ABSTRACT ART mean?

How I proved the Pythagorean theorem, 1

Goldbach calculator, 1

Оградата на Патриарха

Categories

Archives