|
Имат биографии, но нямат постижения. Имат гънки в коремите, но не и в главите. Подписали са се на стотици документи, но не и на един-едничък качествен продукт. Имат усет за морфичния резонанс, но не и за отвращението, което предизвикват. Господи, защо им даде повече, отколкото могат да понесат?
0 Comments
They say there has never been a war between countries that host McDonald’s restaurants. What is harder to realize is that McDonald’s restaurants, so full of people and so unprotected, have never been attacked by terrorists.
I do not know any terrorists and do not attempt to analyze their psychology, but nevertheless think the explanation is obvious. The terrorists do not have issues with democracy, market economy and their "child" called McDonald’s. The terrorists probably have issues with the fact that the democracy and the market economy often visit their countries and homes uninvited (which McDonald's does not). Стремежът на предците беше да се извисят. Стремежът на съвременниците е да се закръглят. Докато предците приличаха на единици, съвременниците приличат на нули.
Приоритетите на националната ни сигурност са затварянето на "читанки" и пушачи на марихуана, но не и затварянето на границите. Разходете се от площад "Лъвов мост" до площад "Света Неделя" и ще се убедите!
The shortest Theory of Success was formulated by Daniel Kahneman. It only consists of two equalities:
success = talent + luck great success = a little more talent + a lot of luck To illustrate Kahneman’s theory let us compare the fate of his with the fate of his friend and collaborator Amos Tversky. They worked and made important discoveries together but it was only Kahneman who became a Nobel prize winner. Tversky did not have the (lot of) luck to live long enough. Our inability to foresee the future does not imply that every imaginable future is possible.
- Какво работиш?
- Писател съм. - Колко книги написа? - Три. - Изкарваш ли пари? - Не съм изкарал и лев. - Че какъв писател си тогава? - Какво искаш да кажеш? Да не би да смяташ че Ван Гог не е бил художник, понеже не е продал нито една картина приживе? - Абе, приживе не е продал, ама след смъртта си е продал десетки. - Да не би да искаш да кажеш че Ван Гог е станал художник след смъртта си? Създателите на Изкуствения интелект са заети с благородната и трудна задача да го научат да разбира че:
а) "Бургаско" пиво се прави в Хасково, а б) "домашното" кисело мляко "Родопчанка" се прави във фабрика, която не е в Родопите. Не можеха ли да се заемат с по-благородната и не толкова трудна задача да научат хората да използват прилагателните консистентно? Да не излезе че е по-лесно да се научи Изкуствения интелект да разбира хорските безсмислици, отколкото да се научат хората да говорят правилно? Фараоните вярвали че пирамидите ще защитят телата и душите им във Вечността. Не знам за душите, но телата им изглеждат беззащитно и глупаво в музейните зали.
Днешните български властници вярват че "техните" магистрали и тротоари им гарантират място във Вечността. Не знам за мястото, но телата им ще изглеждат беззащитно и глупаво в съдебните зали. Днес няма да ядем кюфтета, а ще се мъчим с един проблем от Хенри Дуудни.
Готвач приготвил 5 кутии с кюфтета от кайма и 1 кутия с картофени кюфтета. В кутиите имало 31, 18, 20, 15, 19 и 16 кюфтета, без да знаем в коя били картофените. Синът на готвача запазил за себе си кутията с картофените кюфтета и продал кюфтетата от кайма на двама клиенти, единият от които купил два пъти повече кюфтета от другия. Колко са картофените кюфтета? Преди, хората вярваха че Спасението е в ръцете на Бог. Сега вярват че то е в ръцете на Държавата. Каквото и да му потрябва, човек се реди на опашка пред офис на държавата. Без значение дали става дума за добро (детска градина, училище, университет, работа, пенсия) или лошо (наводнение, смърт, болест или обикновено оплакване от някого).
Секретарката се обажда да ми каже че ме викал Изпълнителният директор. Чудя се какво съм направил, или по-скоро - какво не съм направил. Може би иска да ми подари нещо за Коледа? Не било това, ИД-то ми казва че се налагало да ме "освободи". Понеже 10 години съм се съгласявал с него и не мога изведнъж да се променя, та се съгласявам и този път - казвам му че и аз го чувствам като освобождение. ИД-то ми казва че никак не е доволен от това, което чува. Аз отговарям че съм още по-недоволен от това, което съм чул. Разделяме се малко по-свободни и много по-недоволни. Подсещам се да си запиша в бележника: Свободата няма нищо общо с доволството.
В България, за успех в живота се смята не да дадеш нещо на света, а да вземеш нещо от сънародниците си. Това е житейска философия, споделяна от всеки:
а) от тези, които вземат чужди пари за да си направят банки, б) от тези, които на по-късен етап вземат банките на първите, в) от изхранваните от стотици хиляди работници милиони пенсионери, които си мислят че СЕГА им се полагат пенсии, защото ПРЕДИ, когато са били милиони, са изхранвали стотици хиляди пенсионери. Почина Гошо Пияндето. Бог, ако може, да го прости. Алкохолът не можа.
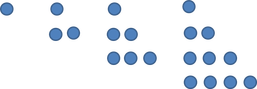
Увод Наскоро, на български излезе книгата "Живата теорема" от Седрик Вилани. Става дума за биографията на една теорема и по-точно – за биография, написана от "бащата" на теоремата. Споменатата теорема е от предния фронт на математиката и по тази причина и тя, а и доказателството ѝ, са неразбираеми не само за обикновените хора, но и за математиците от другите клонове на математиката. Въпреки това, книгата стана бестселър. Кое ли е нещото, направило книгата толкова популярна? Според мен това е идеята за живината на теоремата (и математиката); за това как тя се ражда дълго и мъчително в дългогодишна комуникация между много математици от цял свят; за безсънните нощи, в които е дундуркана подобно на бебе; за радостта и гордостта от израстването на бебето. Макар че думата математика ми звучи на китайски, реших и аз да напиша кратко разказче за раждането на една теорема. Тук става дума за "бременност" продължила 25 века. Тук става дума за комуникация между живи и мъртви хора – каквато е комуникацията между идеите им. Може би разказът няма е толкова интересен, колкото този на Вилани, но съм сигурен че ще е доста по-разбираем. Изложение Около 500 години преди Новата ера, гръцките математици откриват че някои числа са триъгълни. Което означава че те могат да бъдат представени така: Както се вижда от Фигура 1, първото триъгълно число е 1, второто – 3, третото – 6 и т.н. Кое ли е 1234-тото? А n-тото? 200 години по-късно формулата за n-тото число е вече известна: През 17-ти век, френският математик Пиер дьо Ферма открива че ако умножиш произволно триъгълно число по 9 и към резултата прибавиш 1, то полученото число е също триъгълно. Казано с езика на математиката: За n = 1, това лесно може да се провери с помощта на Фигура 1: На математиката ѝ трябваха около 100 години, за да може някой да направи следващата стъпка, т.е. да види че второто събираемо във Формула 2, а именно 1, е също триъгълно число. Направи го Леонард Ойлер, който не спря дотук, а се запита: "А не може ли формулата на Ферма да се обобщи за две произволни триъгълни числа?" Оттук нататък беше лесно, особено за Ойлер: На математиката ѝ трябваха около 250 години за да може някой да направи следващата стъпка, т.е. да усети силата на Ойлеровото равенство и да се запита не важи ли то (или аналогично на него равенство) за други числа. Този някой бях аз, а вторият ми въпрос беше: "Кои са тези други числа?" Ясно беше че те трябваше да са в "роднинска" връзка с триъгълните. Така се насочих към факториалните числа, които са мултипликативният аналог на триъгълните. Казано по-ясно, така както n-тото триъгълно число е равно на сумата на числата от 1 до n, така n-тото факториално число е равно на произведението на числата от 1 до n. Открих равенства при факториалните числа, но те се отнасяха само до сумата на две съседни факториални числа, а не до сумата на две произволни такива. Същото се повтори и с други факториални числа (двойни, четворни и т.н.). В една безсънна нощ четях прекрасното описание на способностите на Айнщайн за аналогично мислене, направено от Дъглас Хофстатър. Изведнъж, моето аналогичното мислене се пробуди и каза: "Тетрахедралните числа". Така както триъгълните числа са суми на последователните естествени числа, тетрахедралните числа (OEIS A000292) са суми на последователните триъгълни числа. Не ми трябваше много време за да открия равенството: където е n-тото тетрахедрално число.
Заключение За да откриеш и докажеш една математическа истина не е нужно да си математически гений или дори математик. И това също е доказателство за живината и силата на математиката. Заблудената държава си мисли че правосъдието е нейн инструмент за налагане на определено поведение на гражданите. Някои заблудени граждани си мислим че правосъдието трябва да е просто една от услугите, които гражданите си купуват (с данъците си) от държавата. Да се докаже кой е по-заблуден!
Популярен блогър започва последното си писание с афоризма "Премиерът има пълното право да е на футболното игрище в работно време, след като и електоратът е бил там в деня на изборите". На пръв поглед афоризмът е мъдър и остроумен. Само дето ...
1. За разлика от електората, на който не му се плаща за да гласува, на премиера му се плаща за да е на работа в работно време (че и извън него). 2. За да има премиер, който спортува през работно време, са виновни НЕ тези, които са спортували по време на изборите, а празноглавците пускали бюлетините така, както пускат водата в тоалетната - без никакво замисляне. Китайците се кланят на равновесието, въплътено в Ин и Ян. Християните и мюсюлманите се кланят на равновесието на Доброто и Злото. Икономистите се кланят на равновесието на търсенето и предлагането.
Отвреме-навреме се намира човек с глава на раменете, който да се усъмни в рационалността на подобни вярвания. Икономистът-нобелист Томас Шелинг казва: Няма нищо особено привлекателно в равновесието. ..... Общественият плаж през лятото е в равновесие когато е толкова претъпкан, че не е привлекателен за този, който иска да отиде на плажа, но не е толкова претъпкан, че хората, които са на плажа да поискат да си отидат вкъщи. ..... Тялото на обесения е в равновесие, когато престане да се клати, но едва ли някой ще каже, че на обесения всичко му е наред. Толкова сме прогледнали, че можем да видим как Вселената ще умре от настинка (т.н. топлинна смърт). Толкова сме слепи, че не можахме да видим как сме довели Земята до изпотяване (т.н. глобално затопляне).
Преди хилядолетие повечето хора бяха селяни и си изкарваха хляба със земеделие и животновъдство. Днес, в селското стопанство на развитите страни работи под 2% от работната ръка. Повече селски стопани не са ни нужни.
Преди столетие мнозинството работещи бяха работници. Бяха толкова силни и многобройни, че си бяха въобразили как бъдещето им принадлежи. Днес, работниците в развитите страни са под 20% от работната ръка. Повече работници не са ни нужни. Преди няколко десетилетия повечето работещи в "развития" западен свят станаха капиталисти. Живееха с убеждението че бъдещето им принадлежи, понеже инвестирането на пенсионните им капитали в капиталистическата икономика ще ги направи милионери след пенсионирането им. Оказа се че толкова капиталисти не са ни нужни, и спихването на капиталовия балон се погрижи за намаляване на броя им. Кои ще са изненаданите от следващия балон? Помислете за голяма група от хора, които вярват че бъдещето им принадлежи! Аз мисля за студентите. Толкова студенти не са ни нужни, което е видно с просто око: бая висшисти продават гащи, чорапи, вестници и застраховки, като в много от случаите дори и с това не се справят добре. Забелязали ли сте какво става, когато тръгнете на гости на дядо си? Можете да се завърнете у вас, т.е. в същата точка на пространството, но това ще стане в друг момент от времето, т.е. в бъдещето. Нещо подобно може да се случи, ако получите възможност да посетите прапрадядо си в миналото:
а) когато се върнете обратно в момента на тръгване, може да се озовете в друга точка на пространството, а не там откъдето сте тръгнали, или б) когато се върнете обратно в точката на тръгване, то може да се озовете там в друг момент от времето, а не в момента в който сте тръгнали. Готови ли сте да поемете този риск, само за да видите прапрадядо си? Изумявам се как хората не правят разлика между интелигентност и креативност. Интелигентността е способността да разбираш дали хората говорят/правят глупости или не, и особено способността да разбираш дали ти говориш/правиш глупости или не. Креативността е способността да правиш:
а) стари неща по нови начини, или б) нови неща. Ако нещата или начините са глупави, то креативността е неинтелигентна. Изумявам се и от начина, по който се третира гениалността. Гледана психометрично (IQ над 140), гениалността е свръхвисока интелигентност. Гледана исторически (постиженията на да Винчи и Айнщайн), гениалността е свръхвисока креативност. Може би гениалността е трето нещо: > специализирана гениалност от тип "Айнщайн" - супер-високи интелигентност и креативност реализирани в малко области, с резултати неразбираеми за широката публика, или > обща гениалност от тип "да Винчи" - високи интелигентност и креативност реализирани в повече области, с достъпни за публиката резултати. Гледам че излязла биография на Майк Тайсън. Защо става така че НЕ се пишат биографии на хора, които са си блъскали главите върху важни проблеми, а на хора, блъскали главите на други хора?
Гледам че излязла биография на Слави Трифонов. Защо става така че се пишат биографии на хора, интервюирали Лий Чайлд, но НЕ и на хора, написали по 20 книги, какъвто е Лий Чайлд? Лий Чайлд ли е по-интересен или тези що го интервюират? Малък брой малки глупаци успяват да направят милиони като продават на голям брой големи глупаци книги и трейнинги със заглавия от сорта на "Как да продадем всичко на всекиго". Никой от глупаците не се сеща че след като си продал всичко на първия, то за другите няма да остане нищо.
|
This website uses marketing and tracking technologies. Opting out of this will opt you out of all cookies, except for those needed to run the website. Note that some products may not work as well without tracking cookies. Opt Out of CookiesCategories
All
Archives
July 2024
|

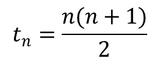
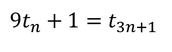
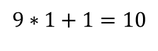
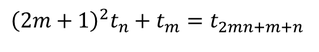
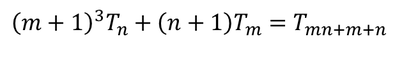
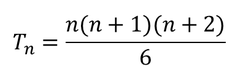
 RSS Feed
RSS Feed
