How many distinct patterns can you create with a thread while sewing on a four-hole button?
Unfortunately, there is no information on the Web what the answer was and had Kolmogorov found it himself. In a book about Grigori Perelman, Masha Gessen admitted that two professional mathematicians, both former students of Kolmogorov, had given different answers.
We found the number of patterns p in several cases where single-color thread was involved. We also found the number of patterns in several cases where threads of different colors c were used, including the case where the buttonholes were located on the vertices of a generic convex n-gon (i.e. a convex n-gon with no more than two diagonals intersecting at any point in its interior). Now, let us try the more complicated case involving different color threads and buttonholes located on the vertices of a “plain vanilla” regular convex n-gon and then generalize our findings with respect to all convex n-gons.
Assumptions:
A1. It is mandatory to utilize the buttonholes. There are many ways to sew on a button without utilizing the buttonholes but let us forget about them for the time being.
A2. All n buttonholes are located on the vertices of a regular convex n-gon.
A3. Different-color threads might be used for different segments between the buttonholes.
A4. Only buttonhole-to-buttonhole connections are used. No cross-border connections are allowed.
Calculation:
1. Some of the regular convex n-gons are generic ones – those, whose number of vertices is an odd number (n = 2*q + 1) plus the square, where n = 4. We have already found (see OEIS A209916) that for the generic convex n-gons the number of patterns p is
p = ((c+1)^((n-1)*n/2) * (c*(c-1))^C(n, 4)) - 1
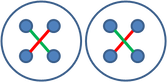
as all possible intersections totaling C(n, 4) must be counted twice when two differently painted diagonals, totaling c*(c-1), intersect (as two different patterns exist for every two colors, which you can see below).
2. Thanks to Bjorn Poonen and Michael Rubinstein and their article “THE NUMBER OF INTERSECTION POINTS MADE BY THE DIAGONALS OF A REGULAR POLYGON” we know some things about regular polygons that we can use now:
a) When n = 2*q the number of diagonals intersecting at a point (except for the center of the n-gon) may be 2, 3, 4, 5, 6 or 7;
b) When n = 2*q the number of diagonals intersecting at the center of the n-gon is n/2.
3. The number of intersection points I(n) of the diagonals can be represented in the following manner: I(n) = i(2)+i(3)+i(4)+i(5)+i(6)+i(7)+i(n/2),
where i(k) (k = 2, …, 7) is the number of points where k diagonals intersect and i(n/2) is the center of the regular n-gon where n/2 diagonals intersect (in the case of n = 2*q, q > 1). Therefore, i(n/2) must be separately counted only in the cases where n = 2*q and q > 7.
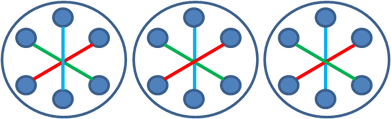
4. In it. 1 above, we saw that two different-color threads (e.g. red and green) look differently when the threads intersect (depending on which one is on top of the other). The same is true when the number of different-color threads is 3, 4 and more (see below how many patterns are there when three differently painted diagonals intersect at a point).
5. Based on it. 2-4 above the formula in it. 1 above takes the following form:
p = (M1*M2*M3) - 1, where
6. This formula could be used for any convex n-gon, as long as we remember that in the cases of n = 2*q + 1, as well as in the cases of n = 2*q and q ≤ 7, we do not need to multiply by the third term (i.e. by M3) as the central intersection point either does not exist (when n = 2*q + 1) or had already been handled (when
n = 2*q and q ≤ 7).
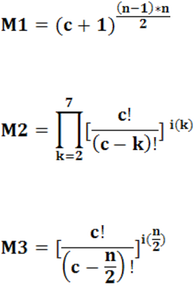
 RSS Feed
RSS Feed
