Goldbach calculator, 1

Insight can emerge from failure to acccomplish something else. Gerd Gigerenzer


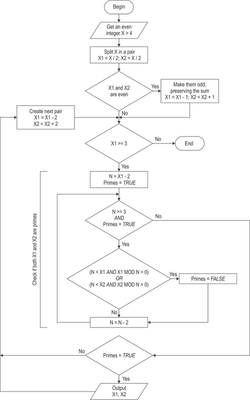
Following my naive attempt to prove Goldbach’s conjecture, I found an algorithm for calculating the Goldbach’s partitions. The calculator you can see HERE is created (based on the same algorithm) by the talented programmer, engineer, photographer and aviation historian Plamen Antonov.

They say a picture is worth a thousand words. See on the left Plamen's picture of my words.
​

Here's my algorithm for the Goldbach calculator:
Step 1. Take Х (an even number greater than 4) and divide it by 2.
Step 2. If the halves X/2 are even go to Step 3,  otherwise go to Step 4.
Step 3. Add 1 to the first half, and subtract 1 from the second half.
Step 4. If X1 and X2 (the numbers resulting from Steps 2, 3 and 5) are prime, print X1 and X2.
Step 5. If X2=3 stop, otherwise add 2 to X1, subtract 2 from X2 and go to Step 4.

---

​P.S. 1
In the language of Wolfram Mathematica my approach

gold[x_]:=Module[{lst={},h=x/2},While[h>1,If[PrimeQ[h]&&PrimeQ[x-h],AppendTo[lst,{h,x-h}]];h--];lst];
gold[1787834]//AbsoluteTiming

works much faster than those based on IntegerPartitions or FrobeniusSolve functions (see the musings of some experts here).​
​
P.S. 2
f[n_]:=PrimePi[n/2]; 
g[n_]:=Module[{lst={}}, Do[If[PrimeQ[n-Prime[i]],AppendTo[lst,{Prime[i],n-Prime[i]}]],{i,1,f[n]}];lst]; 
g[1787834]//AbsoluteTiming

works much faster than its "older sibling" mentioned in P.S. 1.

P.S. 3
June 22, 2020
Who could have known that one day this would be called Ianakiev's Algorithm?