Наскоро, на български излезе книгата "Живата теорема" от Седрик Вилани. Става дума за биографията на една теорема и по-точно – за биография, написана от "бащата" на теоремата. Споменатата теорема е от предния фронт на математиката и по тази причина и тя, а и доказателството ѝ, са неразбираеми не само за обикновените хора, но и за математиците от другите клонове на математиката. Въпреки това, книгата стана бестселър.
Кое ли е нещото, направило книгата толкова популярна? Според мен това е идеята за живината на теоремата (и математиката); за това как тя се ражда дълго и мъчително в дългогодишна комуникация между много математици от цял свят; за безсънните нощи, в които е дундуркана подобно на бебе; за радостта и гордостта от израстването на бебето.
Макар че думата математика ми звучи на китайски, реших и аз да напиша кратко разказче за раждането на една теорема. Тук става дума за "бременност" продължила 25 века. Тук става дума за комуникация между живи и мъртви хора – каквато е комуникацията между идеите им. Може би разказът няма е толкова интересен, колкото този на Вилани, но съм сигурен че ще е доста по-разбираем.
Изложение
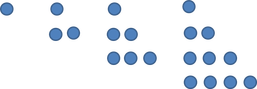
Около 500 години преди Новата ера, гръцките математици откриват че някои числа са триъгълни. Което означава че те могат да бъдат представени така:
Открих равенства при факториалните числа, но те се отнасяха само до сумата на две съседни факториални числа, а не до сумата на две произволни такива. Същото се повтори и с други факториални числа (двойни, четворни и т.н.).
В една безсънна нощ четях прекрасното описание на способностите на Айнщайн за аналогично мислене, направено от Дъглас Хофстатър. Изведнъж, моето аналогичното мислене се пробуди и каза: "Тетрахедралните числа".
Така както триъгълните числа са суми на последователните естествени числа, тетрахедралните числа (OEIS A000292) са суми на последователните триъгълни числа. Не ми трябваше много време за да открия равенството:
Заключение
За да откриеш и докажеш една математическа истина не е нужно да си математически гений или дори математик. И това също е доказателство за живината и силата на математиката.
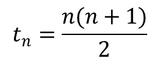
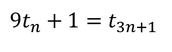
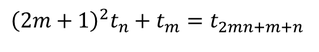
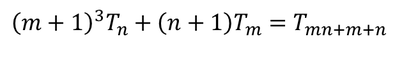
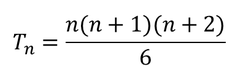
 RSS Feed
RSS Feed
