За читателите с вкус към програмирането бих дал следния пример (на езика Wolfram). Трябва да се дефинира функцията
f[n_]:=Sum[1/Sum[j,{j,1,i}],{i,1,n}]; f/@Range[1000]
а един обикновен математик - това:
f[n_]:=Sum[2/(i*(i+1)),{i,1,n}]; f/@Range[1000]
Когато в нашия пример мислим за яснотата, сред читателите трябва да включим и компютъра, изпълняващ програмата. Един и същ компютър изчислява f[n] за n в интервала [1,1000] по първия начин за 21.3097 секунди, а по втория - за 0.998406 секунди. Накратко: компютърът, слушателите и читателите те разбират добре не просто когато имаш какво да кажеш, а когато знаеш как да го кажеш (защото си си дал труда да помислиш преди да го кажеш). Функцията на математика демонстрира че бързината, красотата и яснотата могат да са в права зависимост. Точно това трябва да е целта ни когато говорим и пишем на родния си език, а и на другите използвани от нас езици.
P.S.
Има различни дефиниции на "добър писател". Някои биха казали че един писател е добър, когато може да впечатли колегите си (а не само публиката). Същото се отнася и до програмистите: добрите програмисти не впечатляват лаиците (които не разбират нищо от работата им), а другите програмисти.
Ако се върнем към нашия пример, дефинирайки функцията така, както го е направил математикът Roozbeh Hazrat:
f[n_]:=Plus@@(1/Rest[FoldList[Plus,0,Range[n]]]); f/@Range[1000]
или така, както бих го направил аз:
f[n_]:=Accumulate[1/Accumulate[Range[n]]]; f[1000]
можем да изчислим f[n] за n в интервала [1,1000] само за 0.374402, съответно за 0.000000..., секунди.
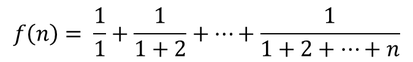
 RSS Feed
RSS Feed
