You have inherited a plot of land and want to build a fence so that no neighbors’ "evil eyes" can pass across the plot. You want to minimize the cost of the fence by minimizing its length. How can you do that?
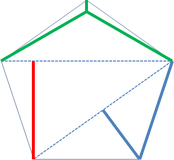
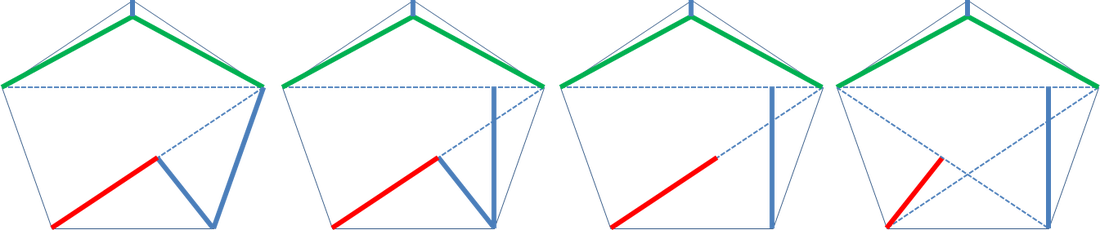
The above is an open mathematical problem. A simple solution will be to approach the problem traditionally and build a fence on every edge of your plot, but it is too costly. On page 21, Fig. 5b of his book Stewart claims to provide the best current solution for the regular pentagon case (see my Fig. 1 below, having in mind that the edges of the pentagon are of unit length and the green lines form the minimum Steiner tree for the three top vertices of the pentagon).
 RSS Feed
RSS Feed
