Happy ending problem: 3+3=5

The Happy Ending Problem is the following simple statement:

Given any five points on a flat surface that are in general position, i.e. no two of them coinciding and no three of them on a straight line, prove that four of these points will always form a convex quadrilateral.

This is the latest proof of mine:
​
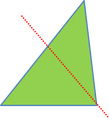
1. Let us start with the observation that a line can intersect three edges of a triangle at most (see below). The number of intersected edges can be zero, two or three, but the number of intersection points can be zero or two (point of entry and point of exit).

2. An edge (or its extension) of a triangle can intersect three edges of another triangle at most (see 1 above). In the extreme case where every edge (or its extension) of the intersecting triangle intersects three edges of the intersected triangle (see below):
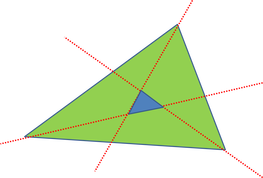
a) The number of intersection points is six, i.e. the maximum, and
b) Any vertex of any of the triangles is collinear with two other vertices, and
c) No edges of the two triangles coincide.

3. As any three points in general position form a triangle, any five points in general position form two triangles sharing a vertex. At least one of the edges (or their extensions) of the intersecting triangle (let us call it a "useful edge") intersects two edges of the intersected triangle at most (otherwise we have a contradiction with the general position requirement, see 2 above). In other words, a useful edge (or its extension) does not intersect at least one edge of the intersected triangle (let us call it a “useless edge”). On the other hand, the useless edge (or its extension) does not intersect the useful edge (otherwise the number of intersection points would be six or more, a contradiction with the general position requirement, see 2 above). Therefore, by connecting this pair of (useful and useless) edges we can build a convex quadrilateral (see below). Q.E.D.